Étude de la variabilité intra-parcellaire de l’azote nitrique et implications en matière d’échantillonnage
Gilles Colinet; Kevin Lefébure; et Christophe Vandenberghe
Résumé
En Wallonie, l’azote potentiellement lessivable (APL), quantité d’azote minéral dans les 90 premiers centimètres de sol en entrée d’hiver, est l’outil de contrôle de bonne gestion de l’azote en agriculture, mis en place pour améliorer la qualité des masses d’eau.
Étant donné l’importance de cet outil de contrôle dans la politique régionale et les répercussions possibles pour les agriculteurs d’un dépassement des seuils établis chaque année, la question de la confiance sur la mesure de ce reliquat azoté apparaît cruciale.
Outre les aspects purement analytiques qui font l’objet d’essais interlaboratoires, la représentativité de l’échantillon de terre sur lequel les mesures sont réalisées est fondamentale. Dans ce cadre, la connaissance de la variabilité de la propriété à l’échelle de la parcelle agricole est un préalable nécessaire pour définir les conditions optimales d’échantillonnage.
Une campagne d’échantillonnage (plus de 130 carottes de sol par parcelle) et de mesure de l’APL a été menée dans deux parcelles représentatives des contextes pédologiques de sols développés sur limons éoliens et de limons mélangés aux matériaux d’altération de roches primaires (grès et calcaires du Condroz). Des outils d’analyse géostatistique ont été appliqués aux résultats et ont permis de déterminer les principaux paramètres de la variabilité spatiale de l’APL.
La réalisation de simulations de différentes modalités d’échantillonnage (nombre de points de prélèvements et type de distribution aléatoire ou non) sur les parcelles permet de les comparer par rapport à leur capacité à fournir un échantillon moyen non biaisé ou compris dans un intervalle de tolérance prédéfini.
Les premiers résultats confirment que les modalités d’échantillonnage retenues en Wallonie (un échantillon composite de 15 carottes) sont conformes à ces exigences pour les exemples étudiés.
Introduction
La maîtrise de la fertilisation azotée dans les agrosystèmes répond à des enjeux tant environnementaux (contaminations des aquifères) qu’économiques (coût des engrais). Le nitrate est un des éléments préoccupants pour la qualité des ressources en eau souterraine à l’échelle européenne. Pour réduire les pollutions par le nitrate à partir de sources agricoles, la directive 91/676/CEE (Directive Nitrates) impose aux États membres de mettre en vigueur des outils législatifs, réglementaires et administratifs .
Entre 2016 et 2019, 7,2 % des sites de contrôle en Wallonie et 11,6 % en zones vulnérables, présentaient une concentration moyenne en nitrate supérieure à la norme de potabilité (50 mg.L-1) (EEW, 2020a). L’azote potentiellement lessivable[1] (APL) est un outil de contrôle de la conformité des exploitations au sein du Programme de gestion durable de l’azote en agriculture qui met en œuvre la Directive Nitrates en Wallonie.
L’APL est la quantité d’azote en kg N-NO3–.ha-1 présente dans le sol en fin de saison agricole. La mesure de l’APL est réalisée chaque année dans 5 % des exploitations choisies aléatoirement. Celles-ci sont déclarées conformes si :
- au moins deux des trois parcelles contrôlées présentent des valeurs d’APL inférieures aux limites de tolérance, établies chaque année pour 8 classes de cultures et prairies sur base de mesures d’APL effectuées dans plus de 250 parcelles d’une quarantaine d’exploitations agricoles de référence et
- aucune des trois parcelles échantillonnées ne présente un dépassement de la limite de tolérance de plus de 100 % et de plus de 100 kg N-NO3–.ha-1 (EEW, 2020b).
Étant donné l’importance de l’APL comme outil de contrôle pour les agriculteurs, son estimation précise nécessite une approche appropriée, c’est à dire qui prend en compte la structure physique de la variable, notamment sa variabilité spatiale et temporelle, à l’échelle des parcelles agricoles.
L’échantillonnage des sols d’une parcelle agricole se réalise généralement par échantillonnage composite. La détermination du nombre de points de prélèvements nécessaire pour assurer un échantillonnage représentatif de la parcelle est toujours source d’interrogation. Des études antérieures ont ainsi permis de proposer des densités idéales et des stratégies de positionnement des points de prélèvement (en diagonale, en aléatoire, sur toute la parcelle, dans une zone homogène etc…). En théorie, le nombre de points de prélèvements nécessaire pour capturer la variabilité spatiale d’une propriété dépend de la variabilité spatiale et de l’imprécision sur l’estimation que l’on est prêt à accepter. Dagnelie (1975) fournit une équation qui met en relation ces données :
où
- n = nombre d’échantillons
- dr est l’erreur relative en % que l’on peut attendre
- CV la variabilité de la propriété exprimée en terme de coefficient de variation en %
- t1-α/2 est la fonction t de Student
En pratique, si on se fixe un niveau de dr acceptable, 10 % par exemple de la valeur cible, et si on mesure la variabilité de la propriété, on peut déterminer l’effort d’échantillonnage. La difficulté principale tient au fait que l’on ne connait a priori pas la variabilité spécifique à une parcelle avant de l’avoir mesurée.
Cette communication traitera de différents aspects liés à la variabilité spatiale de l’APL dans des parcelles agricoles en vue d’en dégager des conseils pratiques d’échantillonnage.
Matériel et méthodes
Méthodologie générale
La méthodologie générale consiste en une analyse (i) de la variabilité spatiale de l’APL dans les sols agricoles, et (ii) des implications en matière de stratégie d’échantillonnage, à travers deux exemples réels et plusieurs cas fictifs.
Les deux cas réels sont étudiés sur des parcelles agricoles de deux régions agricoles différentes en Wallonie avec des APL attendus significativement différents. L’objectif est de déterminer les caractéristiques de la variabilité spatiale de l’APL par une analyse du variogramme, qui met en relation la variabilité spatiale d’une propriété et la distance entre les points comparés.
Ensuite, les variogrammes sont utilisés dans des techniques de simulation par lesquelles on produit par interpolation une série de cartes possibles qui respectent toutes le variogramme mesuré. Des schémas d’échantillonnage aléatoires en 5, 10, 20, 40 ou 80 points sont ensuite appliqués sur chacune des cartes de 4 ha et l’APL est calculé par la moyenne des points d’échantillonnage. Pour chacun des schémas d’échantillonnage, on dispose d’une distribution de valeurs qui permet de quantifier la performance du schéma d’échantillonnage en terme de pourcentage de valeurs dans l’intervalle de précision autour de la vraie valeur de l’APL (figure 1).
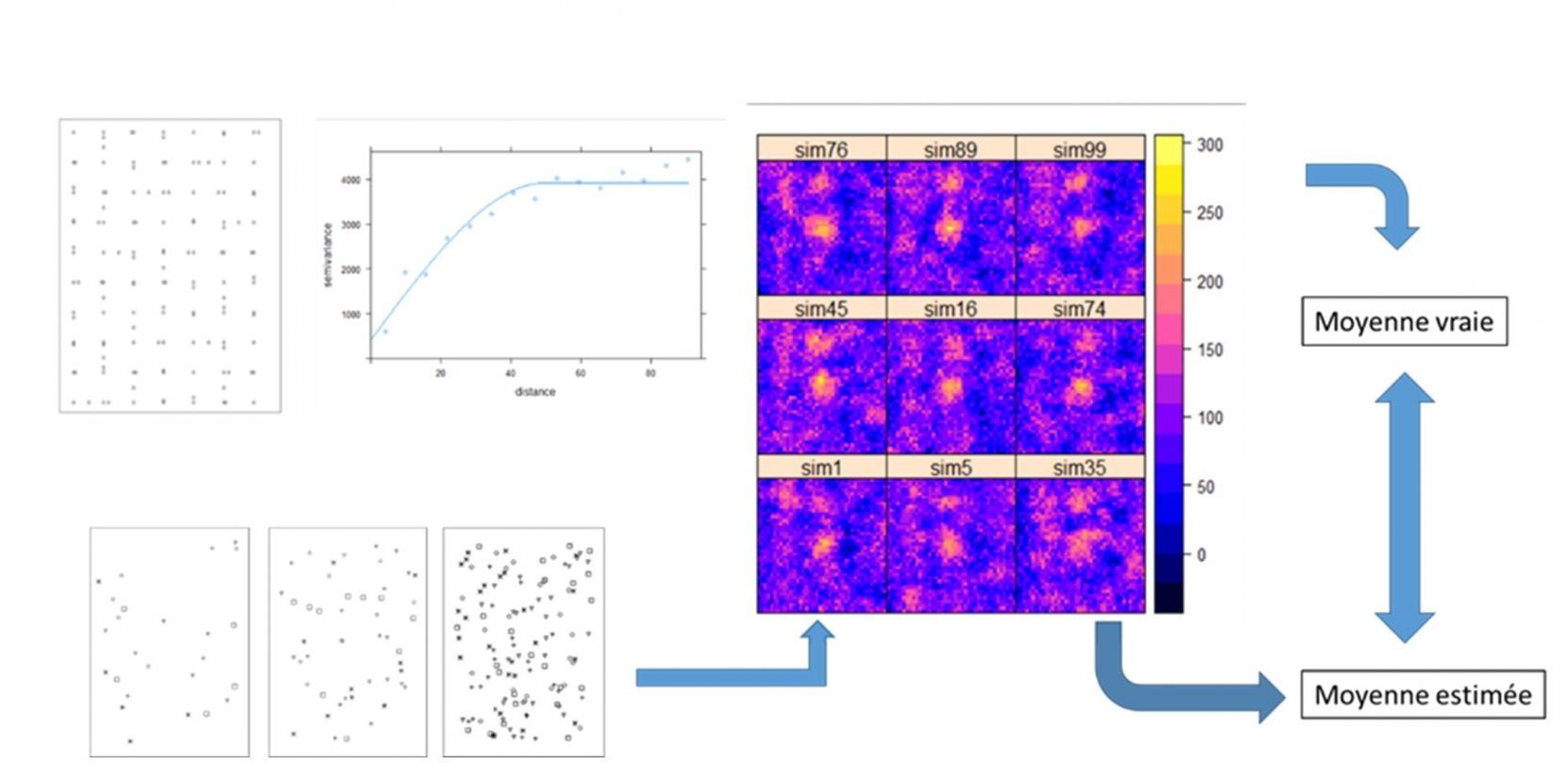
Outre un cas réel, l’exercice de simulation a également été réalisé à partir de cartes fictives construites selon (i) un modèle de distribution spatiale complètement aléatoire, (ii) avec un gradient de teneurs régulier et une composante aléatoire, ainsi que (iii) pour une parcelle avec une zone hétérogène en son centre, pour trois niveaux de teneurs en nitrate (50, 100, 150 kg N-NO3¯ par hectare).
Parcelles étudiées et plans d’échantillonnage
La première parcelle étudiée, dénommée Poucet, est une parcelle de huit hectares en Région limoneuse belge. Elle présente des sols de type limoneux, lessivés à drainage normal, sur les plateaux et les pentes, et des sols sur colluvions limoneuses dans les dépressions. Il s’agit d’un modèle d’organisation des sols classique et la parcelle est cultivée pour la production de froment (Triticum aestivum) et betterave (Beta vulgaris), en rotations, principalement.
La deuxième parcelle, située dans le Condroz, dénommée Biesmerée, présente une association de sols limoneux et de sols limono-caillouteux à charge de silex ou de calcaire.
Les plans d’échantillonnage des parcelles Poucet et Biesmerée ont été établis sur base d’un maillage principal avec une maille de 30 m de côté, auquel des points supplémentaires ont été ajoutés à des distances de 2 m et 15 m à Poucet (figure 2a), 1 m, 5 m et 10 m à Biesmerée (figure 2b). Les surfaces couvertes par le maillage correspondent à environ 6,7 et 4,8 hectares respectivement.
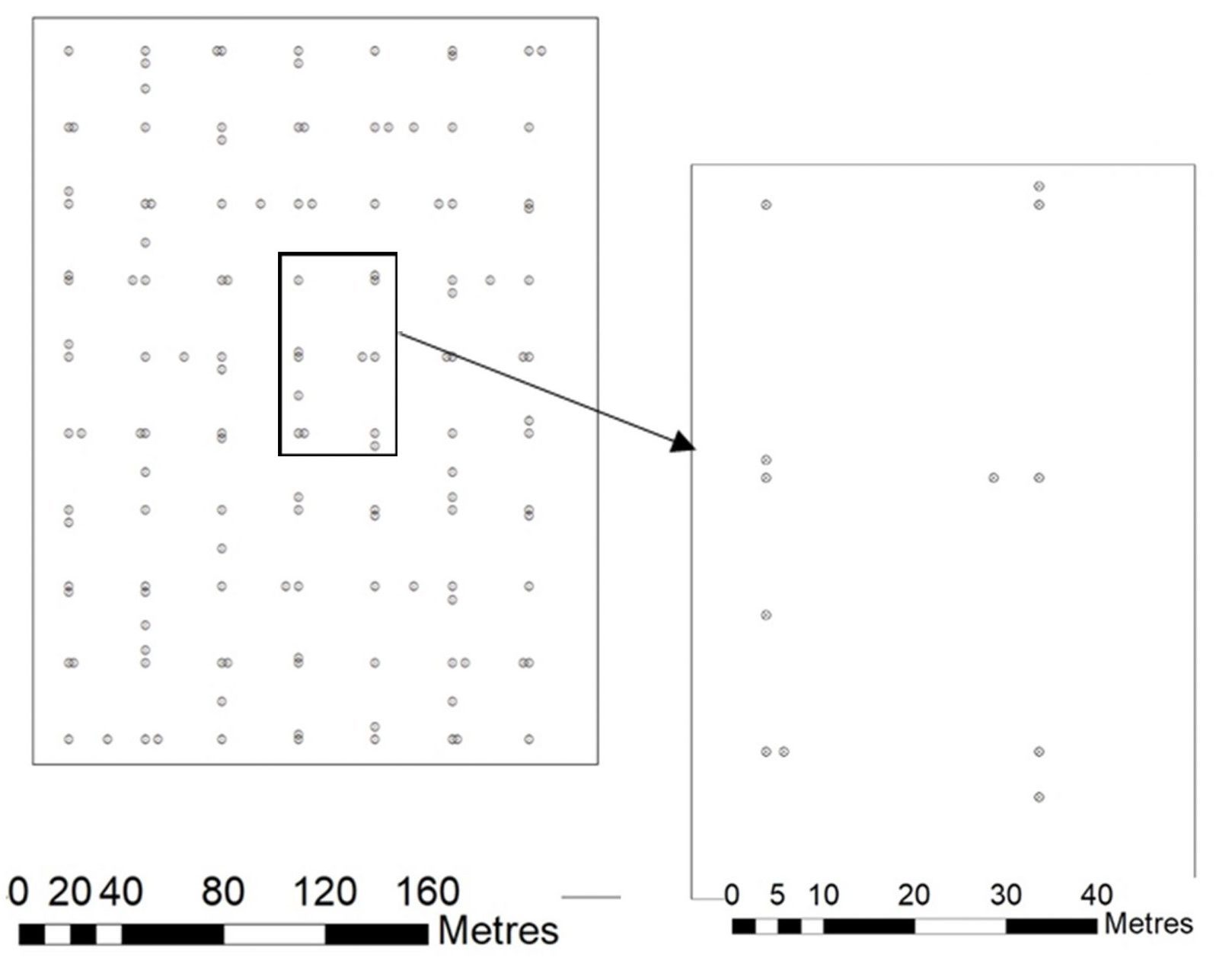
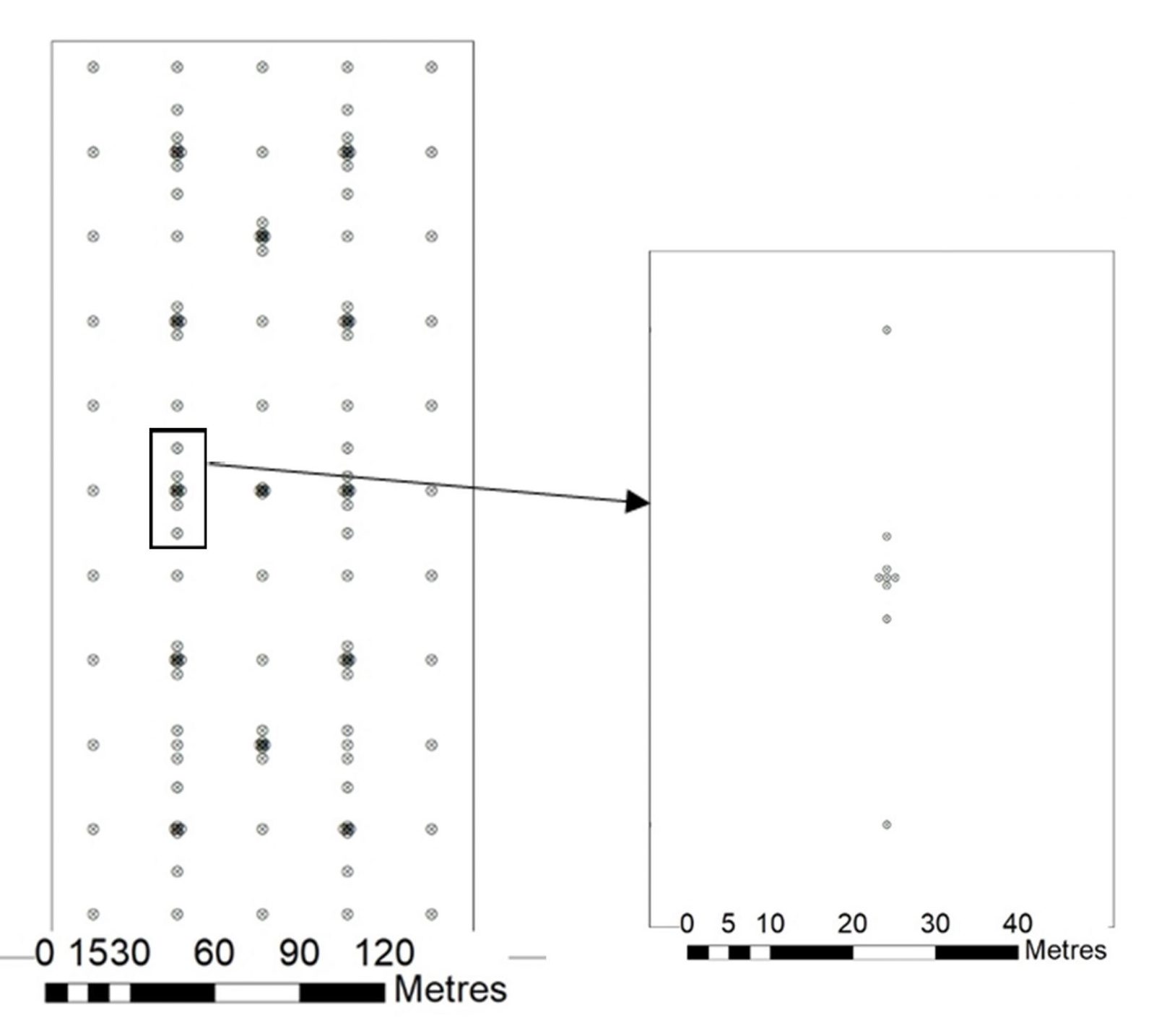
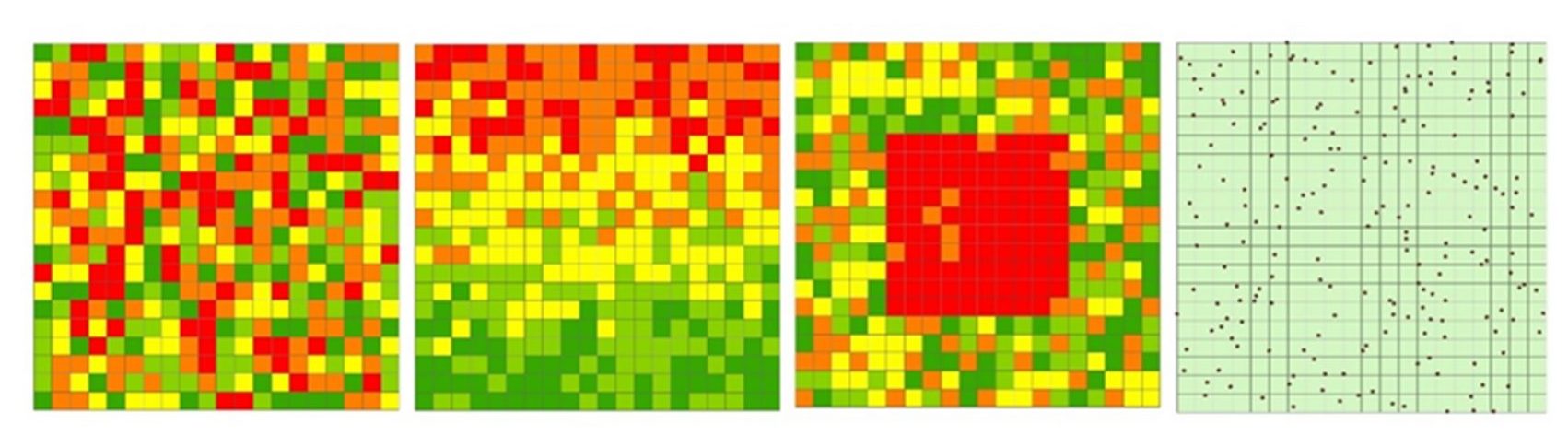
Pour ce qui concerne les parcelles fictives, une grille carrée de 200 mètres de côté divisée en 400 cellules de 20 x 20 m a été élaborée.
Pour les modèles aléatoires, chaque cellule s’est vu attribuer de façon aléatoire une valeur comprise entre 25 et 75, 50 et 150 et entre 50 et 250 kg N-NO3¯.ha-1, pour respectivement les niveaux de teneurs moyens à la parcelle de 50, 100 et 150 kg N-NO3¯.ha-1.
Pour les modèles avec gradient de teneur, la variabilité a été décomposée en un effet d’augmentation linéaire du sud vers le nord de la parcelle et un effet résiduel aléatoire de l’ordre de 20 % de la variabilité totale.
Enfin, des cartes ont été générées en tirant aléatoirement les teneurs comme dans le modèle aléatoire mais en déplaçant dans une zone de 1 ha au centre de la parcelle les 25 % de teneur les plus élevées. L’objectif étant de créer une zone hétérogène au sein de la parcelle. Ensuite, un jeu de 200 points d’échantillonnage a été appliqué aléatoirement pour constituer les points de « mesure » qui serviront à recréer des cartes par simulations (figure 3).
Méthode d’analyse de l’azote
L’APL est mesuré sur échantillons frais, tamisés à 8 mm, selon le protocole de Guiot (1975). Trente grammes de terre sont agités pendant trente minutes avec 150 ml de KCl 0,1M, laissés à décanter trente minutes puis filtrés sur filtre papier Whatman 602H1/2.
Le nitrate d’un ml d’extrait est réduit dans une colonne de réduction Cd-Cu et la concentration en nitrite est mesurée par colorimétrie à 543 nm, après coloration au réactif de Griess-Ilosvay.
Analyse de la variabilité spatiale et krigeage
Pour chacun des jeux de données ponctuelles, un semi-variogramme expérimental a été calculé puis modélisé au moyen du package gstat de R (Pebesma, 2004 ; Gräler et al., 2016). Le semi-variogramme exprime la relation entre le niveau de différence entre deux points voisins et la distance qui les sépare. Le semi-variogramme expérimental est calculé par la semi-variance, c’est-à-dire la moitié de la moyenne des différences élevées au carré, entre toutes les paires de points séparés d’une distance fixée ou le plus souvent dans une gamme de distances. Le semi-variogramme modélisé est une fonction mathématique continue qui s’ajuste au mieux aux points observés et qui sera utilisée pour la prédiction des teneurs, ou krigeage.
Le semi-variogramme (figure 4) peut être défini par le type de fonction, l’effet pépite (niveau de semi-variance pour des distances nulles), le seuil (semi-variance maximale) et la portée (distance entre deux points au-delà de laquelle ceux-ci ne sont plus dépendants spatialement). La différence entre le seuil et l’effet pépite correspond à la proportion de la variabilité qui est structurée spatialement.
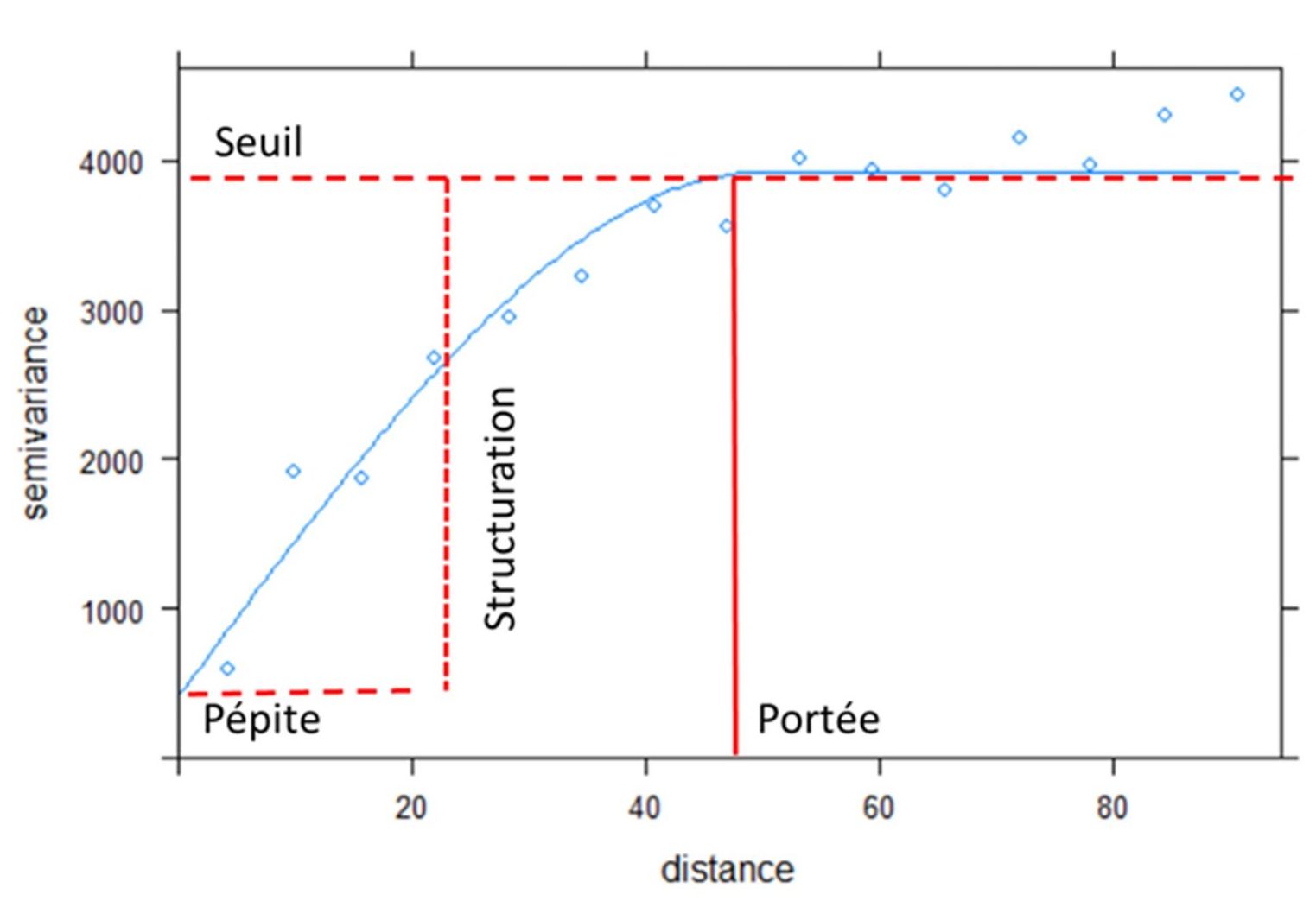
La prédiction spatiale consiste à utiliser les mesures sur des points d’observation pour estimer la valeur de la propriété en un point de l’espace. Le krigeage calcule la pondération à donner aux différentes mesures en fonction de la distance entre les points à partir d’un modèle qui est le variogramme. Le krigeage fournit une teneur estimée ainsi qu’un écart-type qui reflète l’incertitude sur cette prédiction.
L’influence des points de mesure décroît avec la distance selon le modèle choisi et leur position détermine le niveau d’incertitude qui sera associé à la prédiction en un point. Le krigeage fournit donc une teneur estimée et un écart-type qui reflète l’incertitude sur cette prédiction.
Simulations géostatistiques et analyses statistiques
Après la détermination de semi-variogrammes sur base des résultats obtenus sur les différentes parcelles, une collection de 100 réalisations spatiales a été élaborée par simulation géostatistique pour chaque parcelle. Le principe sous-jacent est qu’en chaque point de l’espace la propriété d’intérêt est une variable aléatoire et qu’en théorie, il est possible de générer par interpolation une infinité de cartes qui reproduisent la structure de l’échantillon sur lequel les mesures sont faites.
Les simulations ont été réalisées uniquement sur la teneur en azote nitrique et pour la couche 0-90 cm, qui correspond à la variable utilisée dans le cadre des contrôles APL, sur des cellules de 5 m de côté. Les simulations ont été réalisées sur R à partir du package gstat. La moyenne de tous les pixels des 100 parcelles simulées est considérée comme la valeur vraie de l’APL de la parcelle.
Des dispositifs d’échantillonnage complètement aléatoires ont été appliqués à chaque simulation des différentes parcelles. Cinq niveaux de densité d’échantillonnage ont été retenus, respectivement 5, 10, 20, 40 et 80 points d’échantillonnage pour 4 ha. Pour chaque niveau, 100 tirages de points aléatoires ont été effectués. Pour chaque tirage, la moyenne des 5, 10, 20, 40 ou 80 points est calculée. Au final, pour chaque modèle de parcelles et chaque densité d’échantillonnage, on dispose de 10 000 estimations de la moyenne. Ces estimations sont comparées à la moyenne vraie et la proportion de celles-ci qui sont situées dans un intervalle de 10 % de cette valeur vraie est calculée.
Résultats et discussion
Variabilité spatiale des parcelles Poucet et Biesmerée
Les résultats des analyses sur les parcelles Poucet et Biesmerée sont synthétisés dans les tableaux 1 et 2. Les paramètres variographiques sont donnés au tableau 3.
Il apparaît clairement que les deux parcelles présentent des niveaux d’APL contrastés en réponse aux pratiques agricoles. À Poucet, les sols limoneux sont épais et ont été échantillonnés jusqu’à 120 cm. A Biesmerée, les sols sont moins épais et la tranche 60-90 cm n’a pu être échantillonnée partout.
De manière générale, les niveaux de teneur en azote nitrique sont supérieurs à Poucet (figure 5), quelle que soit la tranche considérée. Ce sont des valeurs qui, si on les compare aux statistiques relatives aux APL en Wallonie, sont dans la gamme haute (Lefebure et al., 2022).
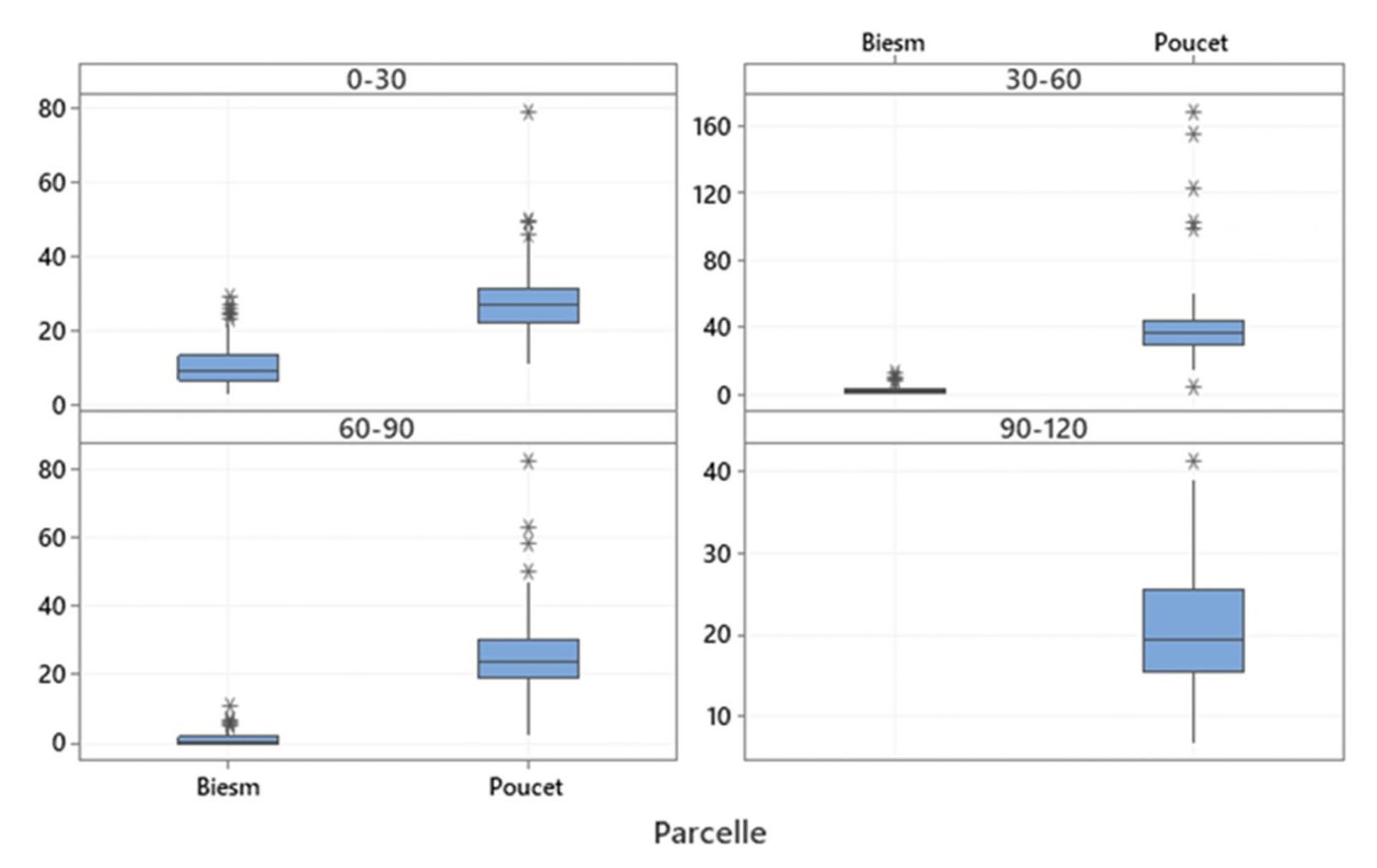
Au niveau de la répartition entre les couches de sol, on constate un maximum dans la couche 30-60 cm à Poucet, tandis que l’essentiel de l’azote nitrique est dans la couche 0-30 cm à Biesmerée. À Poucet, l’azote nitrique est toutefois présent en quantités importantes dans chaque tranche investiguée.
La variabilité des propriétés, exprimée en coefficient de variation, est de l’ordre de 30 à 50 % pour l’azote à Poucet. À Biesmerée, le coefficient de variation est plus élevé, parfois largement au-delà de 100 %. Néanmoins, exprimée en écarts-types, la variabilité est de 2 à 10 fois plus importante dans les sols de Poucet.
Pour ce qui concerne les relations entre les différentes couches de profondeur, on constate pour les deux parcelles que les résultats sont fortement corrélés entre eux et avec l’APL total (tableau 2). Pour Poucet, le coefficient de corrélation avec l’APL est le plus élevé pour la tranche 30-60cm, tandis qu’à Biesmerée c’est avec la tranche 0-30 cm. Quasiment tous les coefficients sont très hautement significatifs, en partie parce que le nombre d’échantillons est élevé (135 et 143 échantillons à Poucet et Biesmerée respectivement sauf pour la couche 60-90 cm à Biesmerée où n = 89). Les corrélations les plus faibles concernent la couche 0-30cm avec les couches 60-90 cm ou 90-120 cm. L’APL total est corrélé de manière plus significative avec les couches 0-30 cm et 30-60 cm.
Tableau 1. Paramètres statistiques (kg N-NO3¯.ha-1) sur l’APL dans les parcelles Poucet et Biesmerée.
| Couche (cm) |
0-30 | 30-60 | 60-90 | 90-120 | APL |
| Poucet | |||||
| Min
Max Moyen. Ec-Ty CV ( %) Média. |
11,0
79,2 28,3 9,6 34,0 27,0 |
4,9
168,4 40,2 20,7 51,4 36,8 |
2,8
82,6 26,2 10,3 39,4 24,1 |
6,7
41,4 20,6 6,4 31,0 19,5 |
42,0
279,2 94,7 33,8 35,7 90,4 |
| Biesmerée | |||||
| Min
Max Moyen. Ec-Ty CV ( %) Média. |
2,6
29,3 10,4 5,4 51,6 9,1 |
0,2
12,6 3,1 2,3 73,3 2,4 |
0,0
10,7 1,4 1,8 129,2 0,8 |
–
– – – – – |
4,7
44,3 15,2 8,5 55,9 12,6 |
Tableau 2. Corrélations et p –valeurs entre les teneurs en kg N-NO3¯.ha-1 par couche de profondeur dans les parcelles Poucet et Biesmerée.
| Couche (cm) |
0-30 | 30-60 | 60-90 | 90-120 | APL |
| Poucet | |||||
| 0-30
30-60 60-90 90-120 APL |
/
< 0,001 < 0,001 < 0,001 < 0,001 |
0,636
/ < 0,001 < 0,001 < 0,001 |
0,362
0,448 / < 0,001 < 0,001 |
0,328
0,369 0,611 / < 0,001 |
0,784
0,929 0,682 0,506 / |
| Biesmerée | |||||
| 0-30
30-60 60-90 90-120 APL |
/
< 0,001 0,009 – < 0,001 |
0,702
/ < 0,001 – < 0,001 |
0,274
0,394 / – < 0,001 |
–
– – / – |
0,934
0,854 0,510 – / |
Il est également intéressant de noter que lorsque l’on rassemble les données des deux parcelles, les coefficients de corrélation entre l’APL total et les différentes tranches de profondeur sont très élevés (supérieurs à 0,900, figure 6).
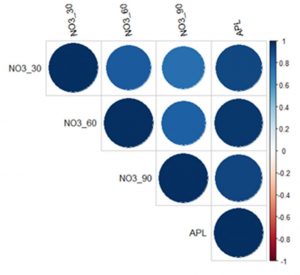
Les teneurs en azote nitrique à Poucet montrent qu’il existe une structure spatiale pour toutes les couches (tableau 3). Les deux premières couches montrent une forte structuration spatiale de la variance (> 70 %) mais se distinguent par des portées contrastées, respectivement 15 m et 52 m. L’APL montre une structure spatiale marquée (80 %) et une portée significative, en relation avec l’azote nitrique contenu dans la couche 30-60 cm qui en est le facteur principal.
Pour la parcelle de Biesmerée, les teneurs en azote nitrique sont caractérisées par une forte structuration spatiale mais une faible portée pour la couche 0-30 cm (12 m) et inversement de plus longues portées pour les couches sous-jacentes mais des effets pépites proportionnellement plus marqués pour les autres tranches. L’APL montre également une combinaison d’une forte structuration spatiale mais d’une faible portée, ce qui rend la cartographie prédictive peu performante.
Tableau 3. Paramètres des semi-variogrammes dans les parcelles Poucet et Biesmerée.
| Couche (cm) | 0-30 | 30-60 | 60-90 | 90-120 | APL |
| Poucet | |||||
| Modèle | Sphérique | ||||
| Pépite
Seuil Portée (m) Struct. |
28
99 15 72 % |
70
590 52 88 % |
83
112 35 26 % |
23
43 58 47 % |
300
1459 48,5 79 % |
| Biesmerée | |||||
| Modèle | Sphérique | ||||
| Pépite
Seuil Portée (m) Struct. |
7,5
25,3 12 70 % |
2,2
2,2 28 50 % |
69
113 25 39 % |
–
– – – |
11
47 10 77 % |
Au niveau de la distribution spatiale des teneurs, le krigeage a seulement été effectué sur l’APL 0-90 cm de Poucet (figure 7). En effet, à Biesmerée, la distribution des points ne montre pas de structure spatiale claire et se rapproche d’une distribution aléatoire. À Poucet, on observe clairement que la portée est de l’ordre d’une cinquantaine de mètres et un effet en taches de concentrations plus fortes ou plus élevées, semblant s’étirer sur l’axe Sud-Nord.
En conclusion partielle, nous ne retiendrons que la parcelle de Poucet pour la suite des applications géostatistiques, celle de Biesmerée n’ayant pas de structure spatiale autre qu’aléatoire.
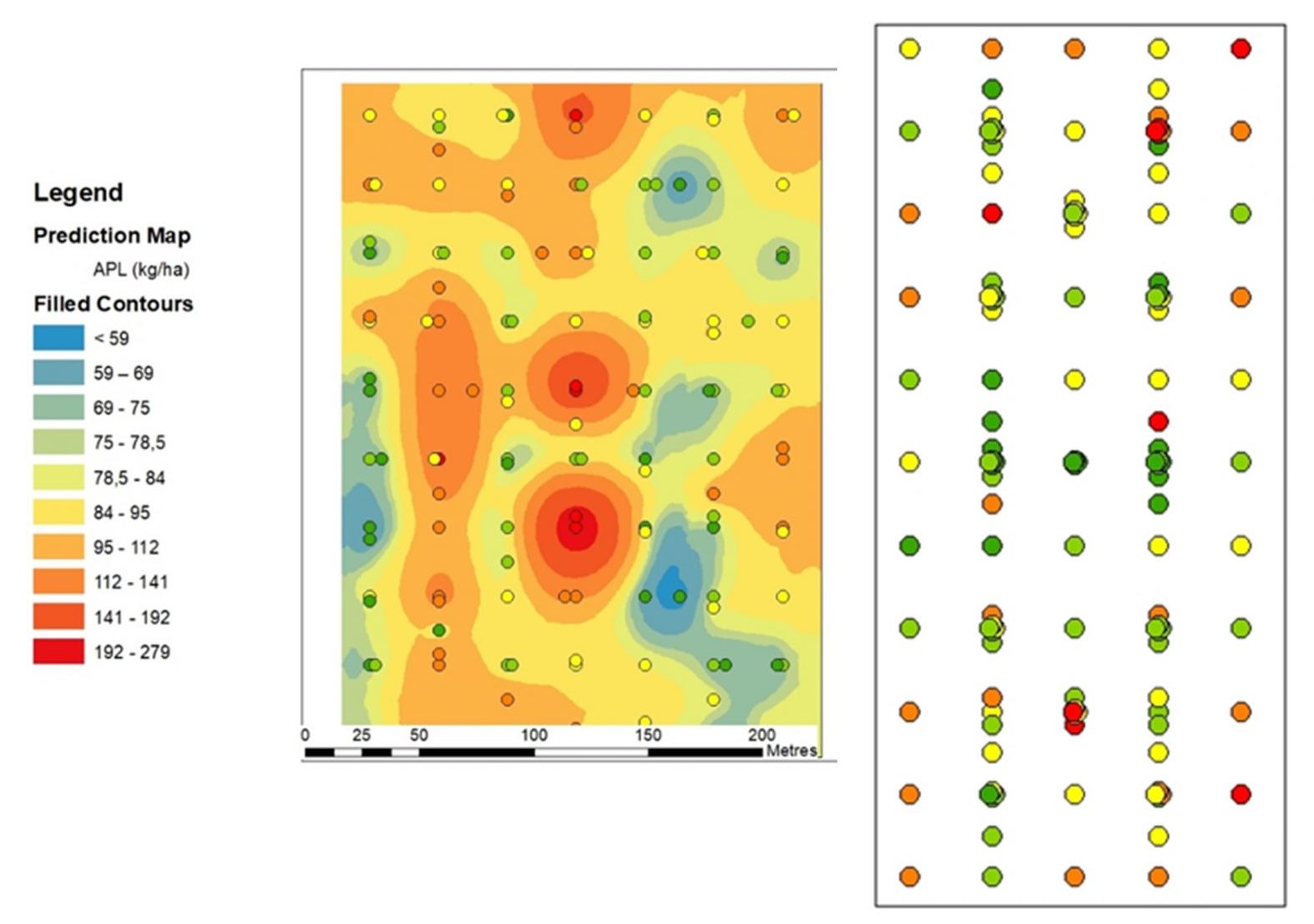
Simulations géostatistiques
Les neuf modèles (aléatoire, gradient, poche à trois niveaux de teneurs 50, 100 et 150 kg N-NO3¯ .ha-1) et la parcelle de Poucet ont fait l’objet de 100 simulations chacune avec krigeage sur une parcelle de 4 ha (200 m x 200 m) avec une résolution de 5 m. Quelques cartes ont été extraites pour illustration à la figure 8.
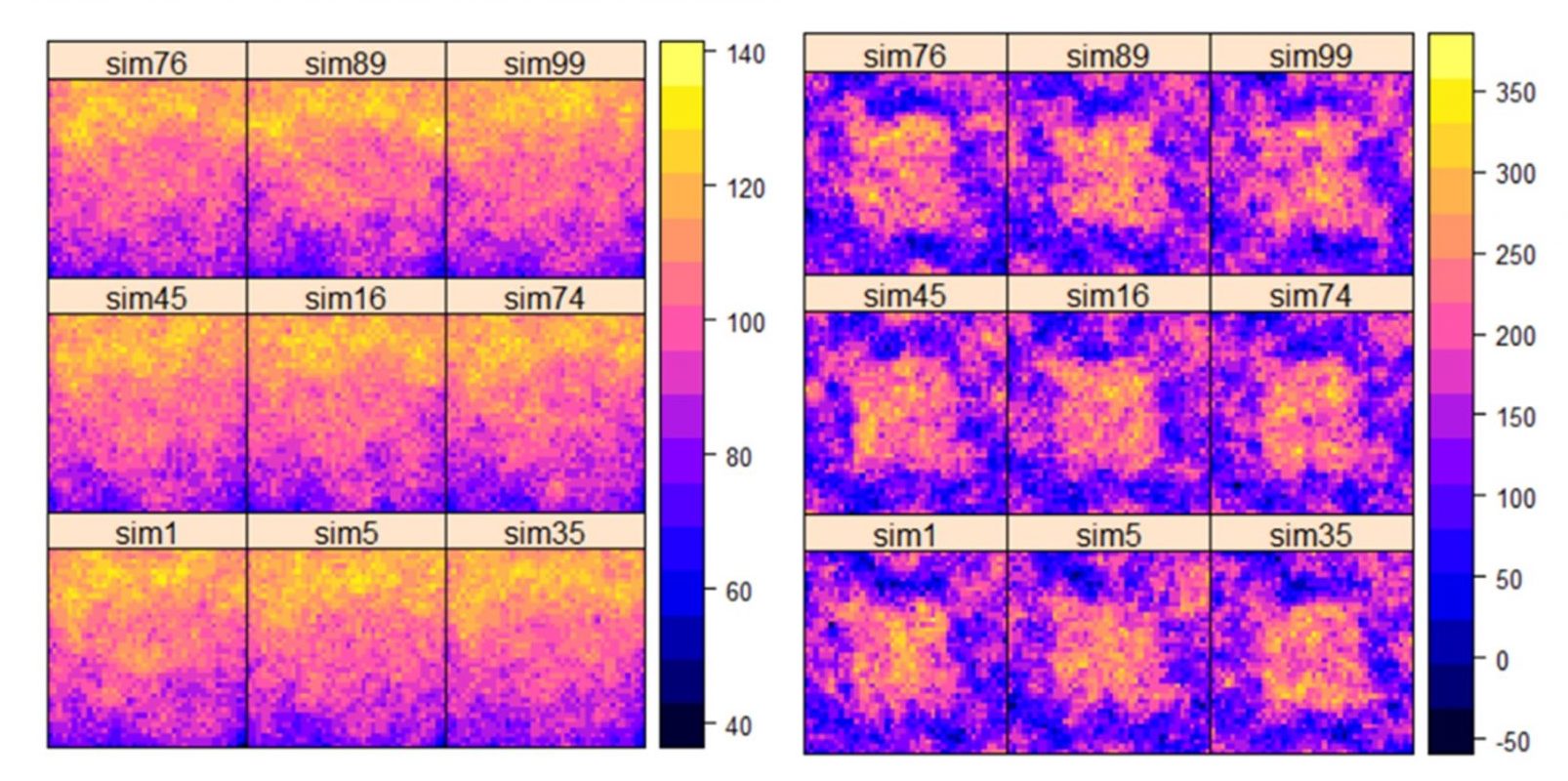
Les paramètres statistiques de base des cartes simulées sont présentés au tableau 4. On notera que les moyennes vraies obtenues par les simulations ne sont pas exactement égales à 50, 100 et 150 kg.ha-1, en raison de la procédure qui consiste à tirer aléatoirement 200 points sur une carte qui contient de la variabilité. On notera également que les écarts-types sont proportionnels aux teneurs moyennes pour un même modèle mais que le modèle en gradient présente une variabilité deux fois moins importante que les deux autres modèles. La parcelle de Poucet présente des niveaux de teneur moyenne et variance similaires à ceux des modèles Gradient_100 et Poche_100.
En termes de semi-variogrammes, les différences concernent davantage les trois types de modèles que les niveaux de teneurs moyennes. Les modèles aléatoires sont caractérisés par de faibles portées, les gradients par les portées les plus longues et des structures spatiales moyennement marquées, tandis que les modèles en poches présentent des portées de l’ordre de 50 m et une forte structuration spatiale. Le modèle Poucet est assez similaire aux modèles à poches.
Tableau 4. Statistiques relatives aux parcelles simulées.
| Parcelles | ||||||||||
| A50 | A100 | A150 | G50 | G100 | G150 | P50 | P100 | P150 | Poucet | |
| Moy
E-T CV |
51
15 29 |
101
28 28 |
144
54 37 |
50
7 14 |
101
13 13 |
153
25 17 |
52
14 28 |
102
32 32 |
155
61 39 |
96
36 37 |
| Limite pour erreur relative de 10 % | ||||||||||
| L lim
U lim |
46
56 |
91
112 |
129
158 |
45
55 |
91
111 |
138
168 |
47
57 |
92
112 |
140
171 |
86
105 |
| Variographie | ||||||||||
| Pépi
Seui Port C/CO |
113
204 38 45 |
428
782 7 45 |
0
2868 12 100 |
6
27 97 78 |
14
110 97 87 |
84
469 106 82 |
15
232 53 94 |
125
1085 48 88 |
417
3924 50 89 |
300
1459 49 79 |
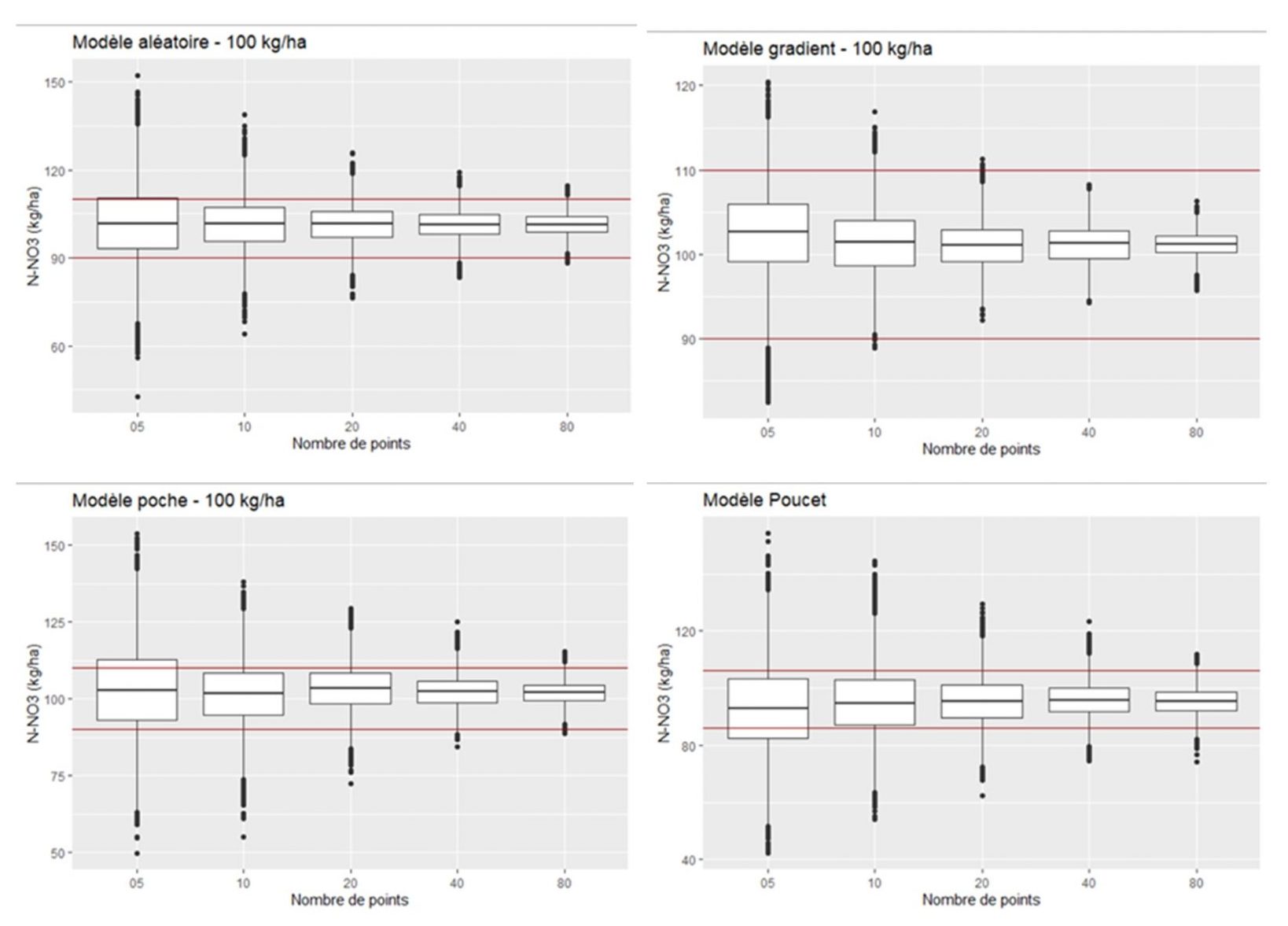
Connaissant la valeur vraie pour chaque modèle, un intervalle correspondant à 10 % d’erreur relative a été défini afin d’évaluer la performance des différents plans d’échantillonnage à prédire cette moyenne (tableau 4).
Cent jeux de 5, 10, 20, 40 et 80 points tirés aléatoirement appliqués sur 100 simulations d’une carte donnent 10 000 estimations de la moyenne pour chaque modèle. La proportion d’estimations comprise dans l’intervalle de ± 10 % d’erreur relative autour de la moyenne vraie est donnée au tableau 5 pour chaque situation.
On constate que les performances des plans d’échantillonnage sont meilleures pour les modèles en gradient par rapport aux autres modèles. En effet, il apparait que déjà les plans à 10 points d’échantillonnage présentent une estimation satisfaisante de la moyenne dans plus de 95 % des cas.
Logiquement, plus le nombre de points d’échantillonnage augmente plus faible est le risque de mésestimer la moyenne (tableau 5 et figure 9). Seuls les modèles en gradients présentent des situations où 100 % des estimations sont considérées comme acceptables. Ces constats sont en lien avec le niveau de variabilité des parcelles. À l’instar de la formule de Dagnelie (1975), le coefficient de variation est bien le facteur qui conditionne le nombre d’échantillons nécessaires pour estimer la moyenne parcellaire. Dans les exemples étudiés, si l’on fixe comme critère que 100 % des estimations doivent être dans l’intervalle d’acceptation, prélever 80 échantillons sur 4 ha n’est suffisant que pour les parcelles à faible variabilité. Si l’on se fixe plutôt des seuils de 95 ou 90 %, alors les schémas d’échantillonnage à respectivement 80 et 40 points peuvent s’avérer suffisants.
Tableau 5. Performance des plans d’échantillonnage ( % de prédictions entre 0,9 et 1,1 autour de la moyenne vraie) et variabilité relative des cartes (CV en %).
| Modèle | APL | Nombre de points | CV ( %) | ||||
| 5 | 10 | 20 | 40 | 80 | |||
| Aléatoire
Aléatoire Aléatoire Gradient Gradient Gradient Poche Poche Poche |
50
100 150 50 100 150 50 100 150 |
55
58 45 91 93 81 58 52 44 |
71
74 60 97 99 94 75 68 59 |
86
88 76 100 100 100 91 82 74 |
97
96 89 100 100 100 98 95 89 |
99
100 96 100 100 100 100 99 97 |
29
28 37 14 13 17 28 32 39 |
| Poucet | 100 | 46 | 59 | 74 | 89 | 95 | 37 |
L’application de l’équation de Dagnelie (1975) à nos jeux de données tendrait à retenir des schémas d’échantillonnage comprenant entre 30 et 40 points, ce qui par l’approche par simulation utilisée ici correspondrait à des mésestimations dans 10 à 15 % des cas. Il y a donc un double niveau de choix à poser : quelle erreur relative est-on prêt à accepter et quel est le pourcentage de mésestimations tolérable ?
La réglementation wallonne impose de réaliser 15 prélèvements par parcelle de moins de 15 ha, ce qui selon les données du tableau 5 amènerait à dépasser l’intervalle des 10 % autour de la moyenne dans 20 à 30 % des cas, hors situations de gradient. Dix pourcents de marge d’erreur sur l’estimation correspond à moins de 10 kg par hectare pour une parcelle comme Poucet. Si l’on accepte une marge d’erreur plus large de l’ordre de 15 kg N-NO3¯.ha-1, une simulation d’échantillonnage avec 15 points de prélèvements aléatoires sur l’ensemble de la parcelle (100 échantillonnages fois 100 parcelles simulées) conduit à une prédiction dans l’intervalle de confiance dans 87 % des cas. Augmenter le nombre d’échantillons à 20 ou 40 par parcelles conduirait à augmenter ce pourcentage à respectivement 92 et 98 %.
Perspectives
Le travail effectué dans le cadre de cette recherche a permis d’investiguer quelques aspects de la variabilité spatiale de l’APL dans les sols cultivés. A Poucet, les résultats montrent que l’APL est structuré spatialement, contrairement à Biesmerée où la distribution des mesures semble aléatoire.
Différents cas d’étude fictifs ont été construits et comparés à la parcelle de Poucet. Les résultats confirment que le niveau de variabilité de la propriété à l’échelle de la parcelle est un facteur essentiel dans la détermination du nombre d’échantillons nécessaires pour caractériser celle-ci. Une approche sécuritaire sur le risque de mésestimer la moyenne d’une parcelle cultivée conduirait à prélever au minimum 80 échantillons sur une parcelle de 4 ha, ce qui n’est pas réaliste à mettre en œuvre. Il n’empêche que la réflexion vaut la peine d’être menée sur la marge d’erreur tolérable.
Pour ce faire, le travail doit être poursuivi au moins à deux niveaux : (i) multiplier les cas d’études réels pour déterminer les niveaux de variabilité qui sont rencontrés sur le terrain et ainsi déterminer les densités d’échantillonnage qui réduisent le plus le risque d’erreur tout en étant gérable et (ii) tester d’autres plans d’échantillonnage tels que pratiqués à certains endroits : échantillonnage en croix, en diagonale, en cercle, etc sur tout ou partie de la parcelle, etc.
Bibliographie
Pebesma, E.J., 2004. Multivariable geostatistics in S: the gstat package. Computers & Geosciences, 30, 683-691.
Dagnelie P., 1975. Théorie et méthodes statistiques. Applications agronomiques. Volume II. Les méthodes de l’inférence statistique. Gembloux, Belgique : Presses Agronomiques de Gembloux.
EEW, 2020a. État de L’Environnement Wallon. Teneurs en nitrates dans les eaux souterraines. Mise à jour 10 décembre 2020. http://etat.environnement.wallonie.be/contents/indicatorsheets/EAU %2013.html#
EEW, 2020b. État de L’Environnement Wallon. Teneurs en nitrates dans les eaux souterraines. Mise à jour 16 décembre 2019. http://etat.environnement.wallonie.be/contents/indicatorsheets/AGRI %209.html#
Gräler B., Pebesma E., and Heuvelink G., 2016. Spatio-Temporal Interpolation using gstat. The R Journal, 8(1), 204-218.
Guiot J., 1975. Estimation des réserves azotées du sol par détermination de l’azote minéral. Rev. Agric., 28, 1117-1132.
Lefébure K., Vandenberghe Ch. & Colinet G., 2022. Analyse des résultats du contrôle APL 2020 et évolution depuis 2008 à l’échelle des masses d’eau souterraine de Wallonie. Rapport. 67p. Gembloux Agro-Bio Tech (Uliège) https://hdl.handle.net/2268/293113
Remerciements
Les travaux qui ont permis la rédaction de cet article ont été soutenus par la Wallonie.
- Même s’il s’agit à strictement parler de lixiviation, le terme « azote potentiellement lessivable » est le terme utilisé dans la règlementation wallonne et sera donc conservé dans ce document. ↵


